Chemical Thermodynamics Chapter 4 Chemistry Class 12 Textbook Solution

Answer:-

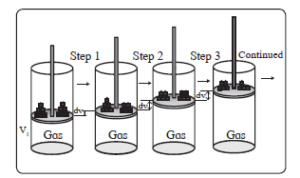
1. Consider \(n\) moles of an ideal gas enclosed in a cylinder fitted with a frictionless movable rigid piston. It undergoes isothermal and reversible expansion from the initial volume \(V_1\) to the final volume \(V_2\) at temperature \(T\). The expansion occurs in multiple steps, as depicted in the figure.

2. When the volume of the gas increases by an infinitesimal amount \(dV\) in a single step, the small quantity of work done is given by:

\[dW = -P_{\text{ext}} dV \quad \text{(1)}\]

3. As the expansion is reversible, the pressure \(P\) is slightly greater by an infinitesimal amount \(dP\) than the external pressure \(P_{\text{ext}}\). Thus, we have:

\[P - P_{\text{ext}} = dP \quad \text{(2)}\]

Combining equations (1) and (2), we obtain:

\[dW = -(P - dP) dV = -PdV + dP \cdot dV\]

Neglecting the product \(dP \cdot dV\) (which is very small), we simplify it to:

\[dW = -PdV \quad \text{(3)}\]

4. The total work done during the entire expansion from volume \(V_1\) to \(V_2\) is the sum of infinitesimal contributions from all the steps. The total work is found by integrating Equation (3) over the limits of the initial and final states, representing the maximum work due to reversibility:

\[\int_{\text{initial}}^{\text{final}} dW = -\int_{V_1}^{V_2} PdV\]

Hence,

\[W_{\text{max}} = -\int_{V_1}^{V_2} PdV \quad \text{(4)}\]

5. Using the ideal gas law \(PV = nRT\), we can express \(W_{\text{max}}\) as:

\[W_{\text{max}} = -\int_{V_1}^{V_2} nRT \frac{dV}{V}\] \[= -nRT \int_{V_1}^{V_2} \frac{dV}{V} \quad (\text{since } T \text{ is constant})\] \[= -nRT \ln \left(\frac{V_2}{V_1}\right)\] \[= -2.303 nRT \log_{10}\left(\frac{V_2}{V_1}\right) \quad \text{(5)}\]

6. At constant temperature, \(P_1V_1 = P_2V_2\) or \(\frac{V_2}{V_1} = \frac{P_1}{P_2}\).

Substituting \(\frac{V_2}{V_1} = \frac{P_1}{P_2}\) into equation (5), we have:

\[W_{\text{max}} = -2.303 nRT \log_{10}\left(\frac{P_1}{P_2}\right) \quad \text{(6)}\]

Equations (5) and (6) represent expressions for the work done in a reversible isothermal process.