chapter 6. CHEMICAL KINETICS class 12 chemistry textbook solution
3. Answer the following in brief.
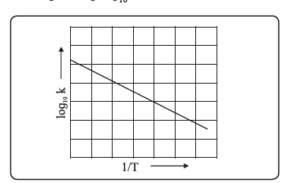
xiv. How will you determine activation energy: (a) graphically using Arrhenius equation (b) from rate constants at two different temperatures?
Answer:-
The Arrhenius equation is given as:
\[k = A e^{-\frac{E_a}{RT}}\]
Taking the logarithm of both sides of the equation, we obtain:
\[\ln k = -\frac{E_a}{RT} + \ln A\]
Converting the natural base to base 10, we write:
\[\log_{10} k = -\frac{E_a}{RT} + \log_{10} A\]
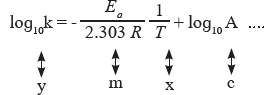
This equation is in the form of a straight line, \(y = mx + c\).
The Arrhenius plot of \(\log_{10} k\) versus \(\frac{1}{T}\) gives a straight line, as shown in the diagram. The slope of the line is \(-\frac{E_a}{2.303R}\) with its intercept being \(\log_{10} A\).
From the slope of the line, the activation energy can be determined.
